С поверхности глобуса на лист бумаги. Поставим перед собой задачу - составить по глобусу карту Африки в цилиндрической квадратной проекции. Масштаб ее по линии экватора 1:50 000 000; густота картографической сетки - 10° по широте и долготе. Прежде всего подсчитаем расстояние между смежными параллелями и меридианами в заданном масштабе. Известно, что длина дуги меридиана и экватора в 1° равна 111 км, а в 10° будет 1110 км. В масштабе карты этому расстоянию соответствуют 2,22 см (1110 км:50 000 000).
На чертежной бумаге проведем две взаимно перпендикулярные линии. Вертикальную линию будем считать нулевым меридианом, а горизонтальную - экватором. Вдоль них через равные интервалы в 22,2 мм проведем параллельные линии, которые образуют сетку квадратов. Континент Африка размещается по широте между 40° с. ш. и 40° ю. ш., а по долготе от 20° з. д. до 60° в. д. Значит, для карты Африки сетка займет 8 квадратов с севера на юг и 8 квадратов с востока на запад. Оцифруем ее и приступим к перенесению контура Африки с глобуса на нашу сетку. Перенос изображений ведется. по клеткам на глаз. Этот способ вам должен быть известен. Вначале намечают точки пересечения береговой линии со сторонами клетки, а затем их соединяют, учитывая изгибы линий. Так же по клеткам можно перенести реки, города и другие нужные нам объекты.
Наличие картографической сетки позволяет проверить точность нашей карты путем нанесения на нее выделяющихся точек по их координатам. В данном случае нанесем крайние точки Африканского континента. Их координаты следующие: северная - мыс Эль-Абъяд (37° с. ш., 10° в. д.); южная - мыс Игольный (35° ю. ш., 20° в. д.); западная - мыс Альмади (18° з. д., 15° с. ш.); восточная - мыс Хафун (51° в. д., 10° с. ш.). Если при нанесении их на карту они попали в соответствующие места, значит, карта составлена правильно.
Из одной проекции в другую. Чаще приходится изготовлять самодельные карты не по глобусу, а по другим картам. Познакомимся и с этим способом. Изготовим, например, карту Гренландии в цилиндрической проекции по исходной карте, составленной в конической проекции (рис. 32, а).

Рис. 32. Карта Гренландии в двух проекциях: а - в конической; б - в цилиндрической
Задача, по существу, сводится к распрямлению дуг параллелей при условии, чтобы меридианы составляли с ними прямые углы. Соотношение сторон каждой клетки картографической сети возьмем 2:1, т. е. отрезок меридиана в 10° будет больше соответствующего отрезка параллели в 2 раза.
Остров в основном укладывается в пространстве от 60 до 85° с. ш. и от 20 до 70° з. д. В этих пределах строим сетку параллелей и меридианов с интервалами в 10° по широте и долготе. Масштаб ее в данном случае произвольный, но если он задан, то интервалы меридиана между 10-градусными параллелями можно вычислить так же, как это делали раньше.
Для повышения точности переноса контура острова можно использовать следующий прием. На исходной карте определяют координаты точек пересечения береговой линии с меридианами или параллелями. Например, 40-градусный меридиан пересекает северный берег острова на широте 83°, а юго-восточный - на широте 65°. Такие точки наносят на картографическую сетку и от них на глаз по клеткам вычерчивают береговую линию со всеми ее подробностями.
При заполнении клеток контурами встречается трудность, ведь трапецию приходится вгонять в прямоугольник и он будет совсем другого размера.
В таких случаях клетки на исходной и составляемой картах обычно сгущают и делают их столь малыми, чтобы можно было на глаз точно скопировать любую фигуру.
Составленная нами карта дана на рисунке 32, б. Конфигурация острова на ней по сравнению с исходной картой изменилась подобно изменению сетки. Например, 80-я параллель распрямилась и намного растянулась. А это привело к тому, что изображение контура острова вдоль этой параллели стало более спрямленным и ширина его увеличилась более чем в 2 раза.
Составим еще одну карту - карту Австралии в цилиндрической проекции, а за основу возьмем карту восточного полушария.
Картографическая сетка для нашей карты будет прямоугольной с соотношением 1:2, например, отрезок меридиана в 10° широты будет соответствовать 2 см, а параллели в 10 долготы - 1 см. Вычертим рамку карты, у ее сторон подпишем широты и долготы соответствующих параллелей и меридианов и
перенесем линию материка.
Сравните очертания Австралии в обеих проекциях. Если на исходной карте общий вид материка соответствует действительной конфигурации, то на карте в цилиндрической проекции изображение получилось сжатым по долготе и вытянутым по широте. И тем не менее в обеих проекциях очертание береговой линии со всеми ее подробностями остается постоянным.
По картам разного масштаба. При составлении новой карты специалисты-картографы в качестве исходного материала нередко используют несколько карт разного масштаба. Попробуем и мы решить такую задачу.
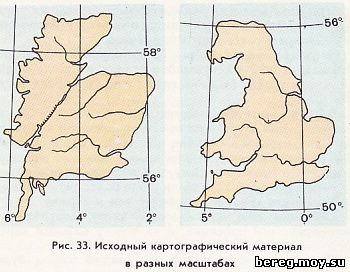
На рисунке 33 даны две карты, составленные в конической проекции. На каждой из них изображен остров, причем на первой карте он кажется более крупным, чем на второй. Но посмотрите внимательно на оцифровку параллелей и меридианов, и вы убедитесь, что масштабы их совершенно различны. В самом деле, на первой карте длина 2-градусного меридиана больше, чем отрезок меридиана в 6° на второй карте. И еще один важный момент: на обеих картах проходит параллель в 56° с. ш. Значит, где-то в этом месте контурные очертания соприкасаются между собой и вместо двух островов получится один. Ваша задача - составить карту этого острова в цилиндрической проекции с соотношением сторон сетки меридианов и параллелей 2:1. Масштаб карты по меридианам 1:11 100 000 (в 1 см 111 км); густота картографической сетки 1° по широте и долготе.
Попытайтесь сообразить, почему мы выбрали масштаб в 1 см 111 км, а не 100. Разумеется, для простоты построения картографической сетки. Вспомните, что 111 км - это протяженность дуги меридиана в 1°. Значит, наша сетка с густотой клеток через 1° будет в виде прямоугольников со сторонами 1Х0,5 см. Такую сетку очень легко построить на листе из тетради в клетку - по две клетки вверх и по одной вправо.
На исходных картах сгустите картографическую сетку, проведя карандашом линии параллелей и меридианов через 1°, и перенесите по клеткам береговую линию с обеих карт на вашу - самодельную. Что же у вас получилось? Оказывается, примерно вдоль 56-градусной параллели контуры обеих карт стыковались и получился единый остров. Нетрудно догадаться, что это Великобритания. Картографическое изображение на рисунке 33, а, превышающее по своим видимым размерам площадь контура, изображенного на рисунке 33, б, оказалось всего-навсего незначительной частью всего острова.
Оригинальные проекции. Картографы могут предложить множество проекций, причем каждая из них будет удовлетворять заданным условиям. Попытаемся и мы решить такую задачу. Допустим, нам потребовалась проекция карты мира, которая имела бы одинаковый масштаб по экватору и по всем меридианам, но в отличие от квадратной проекции, где это условие соблюдается, географические полюсы в нашей проекции должны изображаться точками.
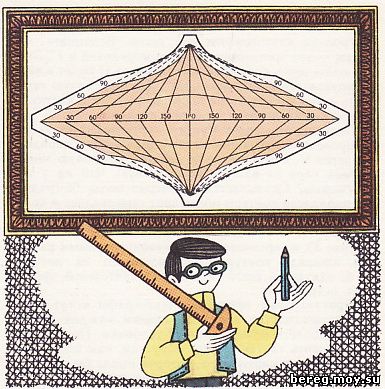
Рис. 34. Проекция для карты с одинаковым масштабом по экватору и меридианам
Для построения картографической сетки в данной проекции проведем линию экватора и отложим на ней равные отрезки, соответствующие определенному числу градусов долготы, например 30° (рис. 34). Через середину линии экватора проведем перпендикулярную линию и отложим на ней вверх и вниз по три таких же отрезка, как и на экваторе. Вершины перпендикуляров соединим прямыми линиями со всеми точками деления на экваторе. Получились меридианы. Согласно условию задачи масштаб по экватору и меридианам должен быть одним и тем же. Чтобы выполнить это условие, отложим на меридианах по три отрезка, равные отрезкам на экваторе. Соответствующие точки на перпендикуляре и наклонных линиях соединим плавными линиями. Эти линии будут параллелями, построенными через 30° по широте. Таким образом у нас получилась картографическая сетка, удовлетворяющая тем же условиям, что и сетка в квадратной проекции, а в вершинах меридианов будут находиться географические полюсы.

Рис. 35. Построение косой азимутальной проекции
Приведем несколько интересных проекций для карт полушарий. Обычные проекции для них получаются путем проектирования градусной сетки глобуса на плоскость, и в зависимости от ее положения могут быть поперечные, нормальные и косые проекции (см. рис. 25). Полушария в косой проекции очень наглядны и часто применяются в учебных целях. Такую проекцию вы можете легко составить сами, используя обычную азимутальную поперечную проекцию полушария (рис. 35). Из центра, находящегося на среднем меридиане недалеко от полюса, проведите окружность так, чтобы она касалась экватора. Меридианы и параллели экваториальной проекции, попавшие в пределы проведенной окружности, обведите, а остальные дорисуйте так, как это сделано на нашем рисунке. Проекция готова, и на нее вы можете переносить контуры материков с глобуса или карты мира.
Мы привыкли видеть карту полушарий в виде окружностей. А нельзя ли картографическое изображение полушария ограничить другой фигурой, например квадратом? Вопрос этот настолько прост, что и не заслуживает внимания. В самом деле, стоит разрезать карту, составленную в цилиндрической квадратной проекции, на две равные части, и у нас получится карта мира, уложенная в два квадрата. Но мы усложним задачу: проекция должна быть такой, чтобы полюсы на карте изображались точками, а не растягивались в прямые линии, как в цилиндрических проекциях. Подумайте, что же нужно сделать. Решение простое: квадрат нужно повернуть на 90° и тогда верхняя и нижняя вершины его будут обозначать полюсы, а горизонтальная прямая, соединяющая две другие вершины,- экватор (рис. 36). Поделим линию экватора на несколько равных частей и точки деления соединим прямыми линиями с полюсами. Эти линии являются меридианами. В нашем примере они проведены через 30° по долготе. Через такие же интервалы проведем и параллели - линии, параллельные экватору. Получилась очень интересная проекция - она равновеликая! Но как в этом убедиться?
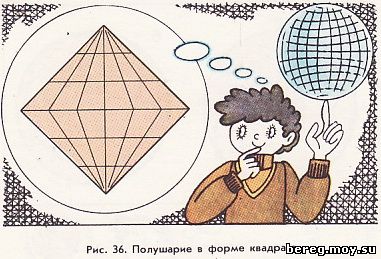
Рассмотрим клетки градусной сетки одного какого-либо ряда, например прилегающего к экватору. Несмотря на их различную конфигурацию, площади их так же, как на глобусе, равны между собой. Доказательство очень простое. Каждая клетка представляет собой трапецию, площадь которой, как известно, равна произведению полусуммы оснований на высоту. А все эти величины согласно построению в каждом ряду равны между собой.
Сравнивая карту северного или южного полушария с глобусом, мы с полной очевидностью убеждаемся в том, что на глобусе дуга меридиана точно равна половине экватора, а на карте ее размер значительно меньше. А нельзя ли построить такую проекцию, чтобы соотношение меридианов и экватора на ней точно соответствовало глобусу?

Рис. 37. Необычные проекции для карты полушария
Путь к решению такой задачи есть: нужно как-то растянуть меридианы. Это сделать нетрудно. Проведем окружность, которая будет обозначать линию экватора. Разобьем длину окружности на восемь равных частей и точки деления соединим пунктиром с центром круга. На каждом пунктирном отрезке построим полуокружности, как показано на рисунке 37, а.
Эти построенные кривые будут обозначать линии меридианов, простирающиеся на 90° от экватора до полюса. В данном случае отрезок каждого меридиана будет составлять 1/4 протяженности экватора. Приведем доказательство:
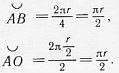
Отсюда следует, что протяженность дуги меридиана будет точно равна половине дуги экватора. Наша задача решена.
Полюс в данной проекции можно сместить вверх, и у нас получится более наглядная проекция - косая (рис. 37, б). Карта в этой проекции очень эффектна. Здесь нам уже кажется, что земной шар не только стремительно летит в безграничном пространстве, но и вращается вокруг своей оси.
Построенные нами проекции создают почву для раздумий. Испытайте вашу сообразительность, и вам самим возможно удастся придумать какую-нибудь свою оригинальную проекцию.
Карта мира на одном полушарии. Возьмите контурную карту западного или восточного полушария и измените на ней оцифровку меридианов. У среднего меридиана, который изображен прямой линией, подпишите 0°, у крайнего правого 180° в. д., у крайнего левого 180° з. д. Подпишите также и соответствующие значения у всех других меридианов. Так без всяких дополнительных построений у вас получилась картографическая сетка для отображения поверхности всего земного шара. Разумеется, искажения материков в такой проекции очень велики: ведь целых два полушария втиснулись в одно! А вот если круг нашего полушария сплюснуть так, чтобы расстояние между полюсами стало бы вдвое меньше экватора, то получится вполне приемлемая проекция. Такую проекцию впервые составил русский ученый Д. А. Аитов, и она получила известность во всем мире.

Рис. 38. Карта мира на эмблеме ООН(а). Звездообразная проекция для карты мира (б)
Определенный интерес представляет собой схематическая карта на эмблеме ООН. Здесь в пределах окружности разместилась вся поверхность земного шара, за исключением Антарктиды (рис. 38, а). Таким образом авторам эмблемы удалось показать олицетворение идей организации, объединяющей все страны, независимо от их политического устройства. Остановимся на этой карте немного подробнее.
Поверхность земного шара от Северного полюса до экватора изображена в обычной прямой азимутальной проекции. А дальше от экватора к Южному полюсу картографическое изображение чрезвычайно искажено. Параллели, уменьшающиеся к югу от экватора, в этой проекции увеличиваются. Понятно, что такая карта для практического использования непригодна. Что же нужно сделать, чтобы проекция стала более реальной? Ответ напрашивается такой. Картографическую сетку от Северного полюса до экватора оставить без изменения, а затем дать разрывы. Так вы и сделайте.
Возьмите циркуль и проведите 6 концентрических окружностей через равные интервалы (рис. 38, б). Окружность, проходящую посередине, примем за линию экватора. Крайнюю окружность поделим на 6 равных частей. Вы, конечно, знаете, как это делать. Раствором циркуля, равным радиусу, «шагайте» по окружности и у вас получится ровно 6 «шагов». Каждую шестую часть крайней окружности поделите еще на 2 части и соедините соответствующие точки прямыми линиями, как это показано на рисунке между точками А и Б. У вас получилась звездоподобная проекция. Параллели на ней изображены в виде окружностей и дуг окружностей, а меридианы - в виде ломаных линий. Дайте оцифровку параллелям и меридианам и приступайте к переносу материков с какой-либо карты мира на эту сетку.



