Главный масштаб. Со странами мира вы впервые познакомились в начальной школе по карте полушарий. В географическом атласе, где помещена, эта карта, указан ее масштаб: в 1 см 900 км. Проверим его. На одном из полушарий измерим расстояние по экватору или по среднему меридиану. Оно составляет 20 см. Это же расстояние в действительности равно 20 000 км. Значит, масштаб карты будет: в 1 см 1000 км. Чем же объяснить такое расхождение?
Для удобства работы картографа ввели понятие «главный масштаб», который относится к определенным местам проекции. Такими местами могут быть точки или линии касания поверхностей, на которые проектируется градусная сетка с глобуса на карту. Для проекции полушария точка касания, называемая точкой нулевых искажений, находится в центре окружности. Непосредственно в точке определить масштаб нам не удастся, но мы можем это сделать на небольшом протяжении в районе этой точки. Для этого измерим здесь длину дуги экватора в 20°. Она получилась равной 2,5 см. В натуре эта дуга составляет 2220 км (20° Х 111 км). Поделим это расстояние на 2,5 см, и мы получим величину масштаба, равную примерно подписанной на карте (в 1 см 900 км).
Вопрос о масштабах очень важный и интересный, и мы рассмотрим его более подробно, используя уже знакомый нам рисунок 27. Все три карты, показанные на нем, составлены в цилиндрических проекциях, а для них характерно касание цилиндра по линии экватора. Следовательно, по экватору и будут считаться главные масштабы для наших карт. Нетрудно догадаться, что в данном случае все карты имеют один и тот же главный масштаб, так как промежутки между 10-градусными меридианами везде равны и составляют 4 мм. Нетрудно также определить и величину главного масштаба. Нам известно, что дуга экватора в 10° на земном шаре равна 1110 км. Этому расстоянию соответствует на карте отрезок, равный 0,4 см. Значит, в 1 см карты содержится 2780 км (1110 : 0,4) и численный масштаб будет выражен отношением 1:278 000 000.
Кроме главного масштаба, на каждой карте имеются частные масштабы. На карте в квадратной проекции (рис. 27, б) частный масштаб по всем меридианам на всем протяжении одинаковый. На карте в равноугольной проекции (рис. 27, в) он будет постепенно увеличиваться от экватора к полюсу, а на карте в равновеликой проекции (рис. 27, а), наоборот, уменьшаться. Частный масштаб по параллелям на всех трех картах по мере приближения их к полюсу резко возрастает, а на самом полюсе им бессмысленно пользоваться, ибо точка, обозначающая полюс, «растянулась» на всю ширину земной поверхности.
Определим частные масштабы для наших карт по 60-й параллели. Чтобы решить такую задачу, нужно знать длины дуг параллелей на разных широтах. Значения их в 1° возьмем из таблицы 1. Протяженность дуги в 10° будет в 10 раз больше и на широте 60° составит 558 км.
Частный масштаб по 60-й параллели на всех трех картах будет один и тот же, ибо отрезки параллелей, заключенных между меридианами, равны и соответствуют так же, как и по экватору, 0,4 см. Поделим действительное расстояние на этот отрезок и получим величину масштаба, равную примерно 1390 км в 1 см (558:0,4), т. е. масштаб будет в 2 раза крупнее главного. Так можно определить частный масштаб, когда он остается постоянным по всей линии. Если же масштаб непрерывно меняется, то мы получим лишь среднюю его величину. Например, на карте в равноугольной проекции (рис. 27, в) отрезок между 60-й и 70-й параллелями в 2 раза больше, чем у экватора. Значит, на этом отрезке средний масштаб крупнее главного в 2 раза.
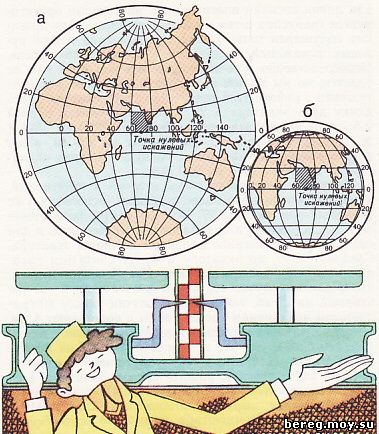
Рис. 30. Карты полушария с одним и тем же главным масштабом
Две карты одного масштаба. В картографической практике не принят термин «средний масштаб» и на всех картах подписывают только главный. Для тех, кто пользуется картой, главный масштаб не всегда понятен, так как он часто не выражает общей масштабности изображения. Обратимся к рисунку 30, на котором показано полушарие в двух проекциях. По виду геометрической поверхности, на которую проектируется сетка глобуса, обе проекции поперечные азимутальные, а по виду искажений одна из них равноугольная, а вторая произвольная. Диаметр полушария в первой проекции вдвое больше, чем во второй. И тем не менее их главный масштаб одинаков. В это трудно поверить, но это так. Приведем доказательства.
В азимутальных поперечных проекциях картографическую сетку переносят на плоскость, касательную в определенной точке экватора, которая является точкой нулевых искажений. Для нее-то и подписывают на карте главный масштаб. Его величину можно определить следующим образом.
Возьмем клетку картографической сетки, расположенную в районе точки нулевых искажений. В первом приближении она имеет форму квадрата и размеры его в обоих проекциях примерно одинаковы. Измерим какую-нибудь сторону квадрата, например ту, которая составляет дуга экватора с разностью долгот в 20°. Она получилась в обеих проекциях равной 0,5 см. Действительное ее расстояние по экватору составляет 2220 км. Значит, масштаб в центральной части той и другой проекции будет равен 1:444 000 000, или в 1 см 4440 км (2220:0,5).
Как неудивительно, но. масштаб, подписанный на этих картах (главный масштаб), будет одинаков, несмотря на разные размеры полушарий.
Универсальный масштаб. На картах обычно дается не только численный, но и линейный масштаб в виде графической шкалы. Понятно, что для карты определенного масштаба строят соответствующую шкалу. А нельзя ли построить один график, который можно использовать для карт разных масштабов? Попытаемся это сделать.
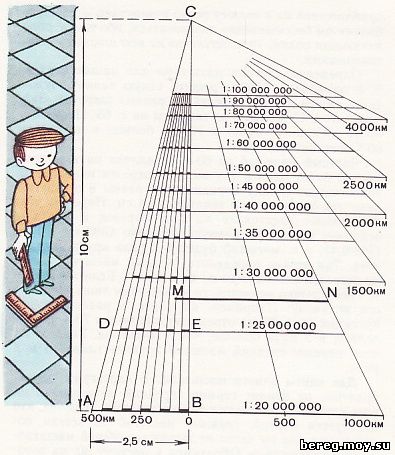
Рис. 31. Универсальный масштаб
Проведем две взаимно перпендикулярные оси и отложим по вертикальной оси вверх отрезок ВС, равный 10 см, а по горизонтальной оси влево отрезок ВА, равный 2,5 см (рис. 31). (Этот последний отрезок будем считать основанием линейного масштаба для карты 1:20 000 000. В этом масштабе он будет соответствовать 500 км. Чтобы найти расстояние СЕ, от которого нужно отложить основание следующего масштаба (1:25 000 000), нужно воспользоваться соотношением. полученным из подобия треугольников АВС и DEC: CB/AB = CE/DE; СЕ = (СВ x DE)/АВ.
Величина DE - основание линейного масштаба - для масштаба карты 1:25 000 000 будет равна 2 см (500 км:25 000 000), а СЕ - 8 см. Таким же путем рассчитываются расстояния от точки С до линий, где будут строиться основания линейных масштабов других карт.
Построенный нами график можно использовать не только для измерения расстояний по картам разных масштабов, но и для определения частного или среднего масштаба карты по любому меридиану и любой параллели. Масштаб карты по меридиану определяется так. Возьмем с карты циркулем-измерителем отрезок меридиана с разностью широт 10°, что будет соответствовать расстоянию 1110 км. Этот раствор циркуля ведем по нашему графику вдоль параллельных линий до тех пор, пока он не уложится в расстояние 1110 км. В нашем случае взятый отрезок MN уложился в расстояние 1110 км между линиями масштабов 1:25 000 000 и 1:30 000 000 (ближе к 1:30 000 000). Значит, частный масштаб карты по данному меридиану получился равным 1:28 000 000.
Чтобы определить масштаб карты по параллели, нужно вначале найти по таблице 1 длину дуги параллели в 10° на определенной широте, а затем порядок действий будет тот же, что и при определении масштаба карты по меридиану.
Наилучший вариант. Когда задача имеет слишком много решений, всегда возникает вопрос, нельзя ли выбрать из нее лучшее. В 1856 году русский математик П. Л. Чебышев поставил и решил следующую теорему для географических карт: найти наиболее подобное изображение данной страны, чтобы искажение масштаба оказалось минимальным. Без доказательства он сообщил, что для этого нужно, чтобы масштаб во всех точках границы страны был одним и тем же. П. Л. Чебышев умер, не опубликовав своей теоремы.
Долгие годы математики всего мира искали это доказательство и, в конце концов, стали сомневаться в правильности утверждения. Лишь в 1896 году русский ученый Д. А. Граве сумел восстановить доказательство Чебышева.
Картографическую проекцию, удовлетворяющую поставленному условию, можно создать только в том случае, когда северная и южная границы страны проходят по параллелям, а западная и восточная - по меридианам. Практически так не бывает. Границы стран обычно проходят по кривым, или ломаным, линиям, не совпадающим с параллелями и меридианами. Тем не менее для каждой страны можно составить проекцию, которая довольно близко подходит к нашему условию.
Идея П. Л. Чебышева нашла практическое воплощение при составлении карт СССР. Такие карты обычно составляют в конической проекции с условием сохранения масштаба по всем меридианам и двум параллелям, одна из которых пересекает южную границу страны, а вторая проходит на несколько градусов южнее побережья Северного Ледовитого океана. Получается так, что конус не касается глобуса, а сечет его по двум заданным параллелям: 47 и 62°.
Возможно, у вас возник вопрос: почему северная параллель сечения, так же как и южная, не пересекает границу страны, а находится южнее ее? Нетрудно догадаться, в чем тут дело. Перенос параллели касания к югу вызван тем, что северные окраины нашей страны слабо обжиты, и поэтому предпочтение в точности картографического изображения отдается местам, более населенным.



