Земной шар в сетке параллелей и меридианов. В приключенческой повести Марка Твена «Том Сойер за границей» описан спор Тома и его друга Гека Финна во время полета на воздушном шаре. Друзья пролетают над Африкой, и Том говорит, что видит на земле длинную ленту, которая тянется по песку, но не может разобрать, что это такое. 

«- Ну вот,- заявляет знаток карты Гек Финн,- теперь ты, может, и узнаешь, где находится наш шар. Ведь это наверняка одна из тех линий, что нарисованы на карте. Те самые, которые называются меридианами. Стоит только нам опуститься вниз и посмотреть, какой у нее номер, и... 

- Ох и болван же ты Гек Финн! Ты что же думаешь - меридианы протянуты по земле? 

- Том Сойер, они нарисованы на карте - ты это отлично знаешь; вот они - возьми сам и посмотри.

- Разумеется, они нарисованы на карте, но это ничего не значит - на земле их нет. 

- Стало быть, эта карта опять соврала. В жизни не видел такого вруна, как эта карта». 

 Как видите, Гек Финн плохо разбирается в карте. Вы, конечно, знаете, что параллели и меридианы - это воображаемые линии проходящие в определенных направлениях: меридианы между Северным и Южным полюсами, а параллели параллельно линии экватора. Сколько же таких линий на земном шаре? На столь простой вопрос не всегда умеют правильно ответить. Многие считают, что меридианов 360 (180 - к востоку о Гринвича и 180 - к западу), а параллелей 180 (90 - к югу от экватора и 90 - к северу). Это совершенно неправильный ответ; их бесчисленное множество. Через любую точку земного шара проходит свой меридиан и своя параллель. 

 Градусная (географическая) сетка на глобусе. Глобус часто называют уменьшенной моделью Земли. И действительно, на нем все материки, океаны и моря показаны в полном подобии с их положением на земном шаре. Как же добились этого, как показали точное положение всех географических пунктов на глобусе? Разумеется, с помощью географических координат. 

 Географические координаты - это широта и долгота, которыми можно указать местоположение любой точки земной поверхности. Например, самая северная точка Азии - мыс Челюскин имеет координаты: 77°43' с. ш. и 104°18' в. д. 

 Координаты считают от линий параллелей и меридианов, которые показаны на глобусе и образуют так называемую градусную сетку. Счет градусов широты ведут, так же как и на земной поверхности, от экватора к северу и югу, а долготы - от Гринвичского меридиана к востоку и западу. 

 Понятия «широта» и «долгота» возникли еще в глубокой древности. Забавно, что эти названия географических координат - результат недоразумения. Просто на одной из самых древних карт, на карте Гекатея Милетского, Земля была изображена в виде овала, длина которого с запада на восток (долгота) в два раза превосходила протяженность его с севера на юг (ширина, широта). 

 С помощью глобуса можно всегда дать правильный ответ на вопрос, какой из двух пунктов южнее или западнее, а какой - севернее или восточнее. Многие, например, считают, что Владивосток находится севернее Ялты и восточнее Хабаровска. Сопоставив параллели и меридианы городов, вы можете убедиться в обратном: Владивосток лежит южнее Ялты и западнее Хабаровска. 

 Шкала для глобуса. Глобус обладает такими свойствами, каких не имеет и не может иметь ни одна географическая карта. Его масштаб постоянный, а следовательно, он сохраняется во всех местах и по всем направлениям. Полное подобие изображения на глобусе с действительными земными очертаниями позволяет определять площади и расстояния, географические координаты, направления на стороны горизонта и т. д. 

 Расстояния по глобусу можно измерять тонкой металлической линейкой или натянутой нитью. Полученное расстояние в миллиметрах затем переводят по масштабу в действительные расстояния в километрах. Нужно только следить, чтобы линейка или нить плотно прилегали к поверхности глобуса и проходили по кратчайшему пути между заданными пунктами, т. е. по дуге большого круга. 

 Удобно измерять расстояния по глобусу с помощью отсчетного кольца, которое можно легко изготовить самим за несколько минут. Узкую полоску толстой бумаги склеивают в кольцо, размер окружности которого должен быть точно равен диаметру глобуса. С внешней стороны кольца на половине окружности наносят 20 делений, каждое из которых будет соответствовать 1000 км (рис. 22, а). Полученные интервалы делят точками на сотни километров. Чтобы измерить расстояние между какими-то пунктами, кольцо надевают на глобус и разворачивают его так, чтобы край шкалы проходил через оба пункта, причем нулевой индекс должен быть совмещен с одним из пунктов. В таком положении отсчет по шкале против другого пункта покажет расстояние между ними. 

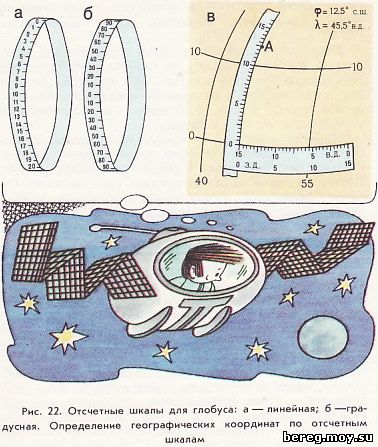
 На второй половине окружности кольца нанесем градусную сетку от 0 до 90 в обе стороны от середины (рис. 22, б). По ней мы будем определять географическую широту пунктов. Снимем глобус с оси и наденем на него кольцо, расположив его так, чтобы край шкалы проходил через центры отверстий, на которые надевается ось, и через заданный пункт, а нулевой штрих совместился бы с линией экватора. Отсчет по шкале против пункта укажет его географическую широту (рис. 22, в). Для определения долготы подклеим полоску бумаги к кольцу против нулевого штриха, как это указано на рисунке. На этой полоске нанесем градусные деления промежутка между двумя соседними меридианами по экватору, причем оцифровка их для восточной долготы должна идти справа налево, а для западной долготы наоборот. В примере на рисунке пункт А имеет следующие координаты: 12,5° с. ш. и 45,5° в. д. Точность определения координат зависит от масштаба глобуса: чем крупнее масштаб, тем выше точность. 

 Градус широты и градус долготы. Географические координаты связаны с дугами параллелей и меридианов, а их можно переводить из градусной меры в линейную и, наоборот, из линейной в градусную. Подсчитаем протяженность дуги меридиана в 1°. Принимая форму Земли за шар радиусом 6370 км, получим величину дуги, равную примерно 111 км. (2 х 3,14 х 6370)/360°. 

 Если два пункта находятся на одном и том же меридиане, то, определив их широты, можно узнать расстояния между ними. Так, Москва и Аддис-Абеба имеют примерно одну и ту же восточную долготу: 38°, а широты соответственно 55,8 и 9,1° с. ш. Разность их составляет 46,7°. Значит, расстояние между городами будет равно примерно 5180 км (46,7 х 111). Чтобы убедиться в правильности наших расчетов, определите это же расстояние по глобусу с помощью отсчетного устройства. 

 Но Земля представляет собой несколько сплюснутый шар и по этой причине дуга в 1° широты на всем протяжении меридиана не одинакова. На экваторе она составляет 110,6 км, а на широте от 78 до 90° будет равна 111,7 км. И если какой-то пункт находится на широте 45°, то оказывается, что он отстоит от Северного полюса на целых 36 км дальше, чем от экватора. 

 Что касается параллелей, то их расстояния между двумя смежными меридианами по мере удаления от экватора становятся все меньше и меньше и на полюсах принимают нулевые значения. Длины дуг параллелей в 1° на разных широтах приведем в следующей таблице:

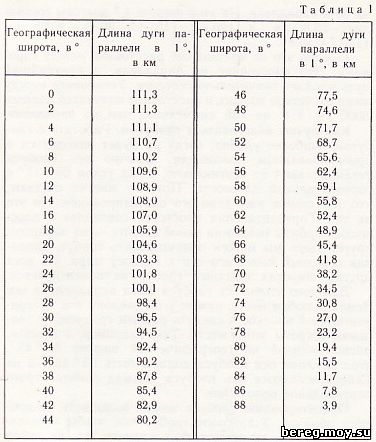
 С помощью таблицы можно решать интересные задачи, и мы будем обращаться к ней еще не раз. А сейчас, используя помещенные в ней данные, определим расстояние между пунктами, расположенными на одной и той широте. Например, Ленинград и Магадан, имеющие восточную долготу 30,4° и 151,1°, лежат примерно на 60-й параллели. На этой широте 1° долготы составляет 55,8 км, а 120,7° (151,1 - 30,4) - 6735 км (120,7 Х 55,8). 

 Однако это не кратчайшее расстояние между городами. Это расстояние по параллели, а кратчайший путь пройдет значительно севернее. Установите между ними отсчетное кольцо, и расстояние получится равным 6000 км, т.е. на 735 км меньше, чем по параллели. 

 Как лучше пользоваться глобусом. Работать с глобусом наиболее удобно, когда он будет находиться в ориентированном положении. Обычно ось глобуса устанавливают не вертикально, а под углом 66°33' к горизонтальной плоскости. Поэтому многие считают, что тем самым уже дано его ориентирование. Но это не так. Горизонтальная плоскость совпадает с плоскостью орбиты только на одной широте - на полярном круге. Здесь мы можем ориентировать глобус, направив северный конец его оси к Полюсу мира. На всех других широтах обычный глобус не ориентируется. 

 Для того чтобы ось глобуса была параллельна оси Земли в любом месте, нужно угол наклона оси к горизонтальной плоскости сделать равным градусному значению широты этого места. Так, например, в Москве, расположенной на географической широте 55°45', угол наклона оси глобуса должен быть 55°45', а на Северном полюсе ось глобуса должна занять строго вертикальное положение. 

 Ориентирование глобуса можно выполнить следующим образом. Установите глобус так, чтобы населенный пункт, где вы живете, был в зените, т. е. на самом верху. В таком положении подложите под основание глобуса какой-нибудь предмет, и он будет ориентрован. Впрочем, подставку вы можете сделать заранее из тре-угольного бруска. Угол наклона на этом бруске должен соответствовать разности величины угла наклона оси глобуса и значения широты вашего населенного пункта. Если, например, вы живете на широте Москвы, то разность составит примерно 11° (66°33' - 55°45'). 

 А как же ориентировать глобус на экваторе и тем более в странах южного полушария? Тут уже такой подставкой не обойдешься. Чтобы, например, определить координаты антарктических станций, нужно переворачивать глобус, придерживая его за основание. Попробуйте в таком положении выполнять на нем какие-либо измерения! В данном случае предлагаем воспользоваться следующим советом. Открутите винт, скрепляющий глобус с осью, выньте глобус и установите его на специально изготовленной подставке в виде широкого цилиндрического кольца (рис. 23). Такую подставку можно легко и быстро изготовить из мягкого картона или толстой чертежной бумаги. Размер окружности кольца должен быть примерно равен окружности 40-градусной параллели глобуса. Кольцевая подставка будет служить очень хорошим приспособлением для работы с глобусом в любой его части. 

Рис. 23. Ориентирование глобуса на цилиндрическом кольце

 Наше приспособление дает возможность произвести ориентирование глобуса для любого географического пункта. Разворачивая глобус в кольце, мы можем устанавливать его в такое положение, чтобы хорошо обозревать любой материк, любую часть акватории и выполнять в этих местах необходимые измерения. 

 Насколько точна модель? Глобус служит замечательным пособием по географии. Глядя на него, можно судить о форме Земли, о вращении ее вокруг оси, видеть угол наклона земной оси к плоскости орбиты и обозревать в уменьшенном виде всю поверхность нашей планеты. Глобус наилучшим образом отображает фигуру Земли и дает правильное, наглядное представление о нашей планете. Все это так. Но не допускают ли картографы ошибки при построении глобуса? Ведь земной шар как геометрическая фигура представляет собой эллипсоид, т. е. несколько сплющенный шар, а фигуру глобуса делают в виде точного шара! Насколько же велики искажения за счет допуска и как бы выглядел глобус, если при его изготовлении учитывать сжатие Земли? 

 В вертикальном разрезе земной шар представляет собой слегка вытянутую окружность, радиусы которой составляют: экваториальный - 6378 км, полярный - 6357 км. Попытаемся изобразить такую фигуру в масштабе 1:20 000 000. Для глобуса это довольно крупный масштаб; диаметр его составит более 60 см. В данном масштабе определим значения радиусов. Они будут соответственно равными 31,9 и 31,8 см. Вычертим взаимно перпендикулярные оси и на них отложим полученные значения. Из точки пересечения осей проведем окружность экваториальным радиусом. Она пройдет всего на 1 мм от точек, обозначающих географические полюсы. Понятно, что такая малая величина не повлияет на точность изображения материков и океанов. Рельеф земной поверхности также не выражается в данном масштабе. Гора Джомолунгма (Эверест) - величайшая вершина Гималаев - представляла бы песчинку высотой около 0,5 мм. 

 На космических снимках форма Земли - идеальный шар. Полярное сжатие и тем более все неровности земной поверхности не сказываются на ее очертаниях на снимке. Такое пояснение необходимо сделать в связи с преувеличением роли полярного сжатия и неровностей земной поверхности.