Это стоит запомнить. Мы уже сообщали раньше, что протяженность дуги меридиана в 1° составляет примерно 111 км. Это число легко запомнить, так как оно состоит из одних единиц. Поделим его на 60 и получим еще одно число - 1,85 км. Нетрудно сообразить, что в результате деления получилось расстояние, соответствующее дуге меридиана в 1'. Это значение (точнее, 1,852 км) моряки приняли за единицу измерения расстояний и назвали ее милей. Такой единицей очень удобно пользоваться в морском плавании. Мили легко переводятся в минуты географической широты, и, наоборот, по разности широт можно сразу же узнать расстояния в милях.
Измерения Гулливера. Вспомним,- как Гулливер, попав в страну великанов, определил размеры ее столицы - города Бробдинжета. Он рассказывает:
«Я сам произвел эти измерения на карте, составленной по приказанию короля и нарочно для меня разложенной на земле, где она занимала пространство в 100 футов. Я прошел несколько раз по диаметру и окружности карты, сосчитал число моих шагов и без труда определил по масштабу точное протяжение города».
Измерив таким путем расстояние по карте, Гулливер узнал, что столица Бробдинжет составляет в длину около 54 миль. А каков же масштаб этой карты?
Полагаем, что протяженность (длина) города измерялась по диаметру окружности, в пределах которой он расположен. По нашим данным, диаметр составляет: на карте - 100 футов, а на местности - 54 мили. Переведем футы и мили в метрическую систему: 100 Х 30,5 = 3050 см, 54 Х 1852 = 100 008 м.
Поделив действительное расстояние (100 008 м) на число сантиметров карты (3050 см), узнаем ее масштаб. Получается, что в 1 см карты содержится примерно 33 м, и численный масштаб будет выражен отношением 1:3300.
Такой масштаб весьма крупный. Обычно планы городов составляют в масштабе 1:10 000 и мельче. Здесь автор, видимо, умышленно увеличил масштаб карты, чтобы поразить читателя ее необычно крупными размерами.

Как измерить расстояние? Что же тут сложного, скажете вы, наложим отмеченный отрезок на шкалу масштаба и мы сразу же узнаем действительное расстояние. Все это так. Но чаще приходится измерять расстояния не по прямым, а по кривым или извилистым линиям, например протяженность маршрута, длину реки, береговую линию озера и т. п. В таком случае можно использовать различные приемы. Возьмем, например, небольшой раствор циркуля-измерителя (обычно 0,5 см), который называют шагом. Одну иглу циркуля установим в начальную точку, а вторую - на измеряемую линию. Поворачивая циркуль вокруг каждой иглы, «шагаем» по линии. Общая длина ее будет равна числу шагов, умноженному на величину шага циркуля, плюс остаток, измеренный по масштабу.
Если кривые плавные, то можно поделить их на ряд отрезков, достаточно малых, чтобы можно было пренебречь разницей между длиной хорды и длиной дуги в каждом из них. В этом случае измерение кривой линии сводится к измерению ломаного контура. Можно также непосредственно прикладывать к пологой кривой линии линейку с миллиметровыми делениями, поворачивая ее по линии так, чтобы она все время по возможности оставалась касательной к кривой. Этот чрезвычайно простой и удобный способ при некоторой тренировке дает благоприятные по точности результаты.

Рис. 39. Измерение протяженности реки с помощью палетки
Познакомимся еще с одним, довольно интересным способом - это измерение с помощью палетки. Ее делают из прозрачной основы, на которую наносят сетку квадратов, стороны которых составляют 3,8 мм (эта величина установлена опытным путем). При определении длины линии палетку накладывают на карту так, чтобы ее стороны были параллельны рамкам карты, а концы измеряемой кривой (точки А, В) оказались внутри сетки (рис. 39, а). При таком положении подсчитывают число сторон квадратов, пересекаемых измеряемой линией. Затем сетку поворачивают дважды: вначале на угол примерно 30°, а затем на угол 60° (рис. 39, б, в) - и при обоих положениях также подсчитывают число пересечений измеряемой линии со сторонами квадратов. Сумма всех пересечений при трех положениях палетки составит длину измеряемой линии в миллиметрах.
Измерения расстояний выполняют по картам, на которых искажений практически нет или они почти незаметны. К ним относятся прежде всего топографические карты, а также карты районов, областей, краев, союзных республик, отдельных небольших государств, протяженность которых с юга на север или с востока на запад не превышает 1500 - 2000 км. По мелкомасштабным картам кратчайшее между двумя пунктами расстояние можно определить по их географическим координатам, применяя довольно сложные формулы. С достаточной точностью и сравнительно легко расстояния по мелкомасштабным картам можно определять вдоль меридианов или параллелей по разности широт или долгот между начальной и конечной точками. Определим этим способом протяженность Каспийского моря с юга на север по меридиану 50°. Для этого снимем с карты географические широты точек пересечения береговой линии моря с 50-градусным меридианом. Они получились равными 46,5° и 37,5° с. ш. Разность их составляет 9°, что соответствует расстоянию 999 км (9х111). Это расстояние (округлено 1000 км) соответствует длине Каспийского моря от устья Волги до берегов Ирана. Его можно использовать при изучении Европы и Азии в качестве сравнительного эталона для глазомерной оценки расстояний между различными пунктами. Подобные эталоны можно наметить и для других стран света. Например, для Африки - длина Красного моря - 2000 км, для Северной Америки - длина полуострова Калифорния - 1200 км, для Австралии - длина полуострова Кейп-Йорк - 800 км.
На морских картах, которые строятся в проекции Меркатора, нет линейного масштаба. Его роль выполняет восточная или западная сторона рамки карты, представляющая собой меридианы, разбитые на деления через 1' по широте. Отсчет расстояния между двумя точками в минутах меридиана покажет действительное расстояние в морских милях.
Каким бы способом мы не измеряли расстояние по извилистым дорогам, оно не будет соответствовать действительному расстоянию. В этом легко убедиться проверкой результатов по спидометру автомашины: расстояние по карте окажется меньше, чем показание спидометра. Чем же вызваны такие расхождения?
Карта не является точной копией местности. Топографы и картографы при съемке и составлении карт производят обобщения отдельных элементов местности. В частности, на извилистых дорогах небольшие извилины и повороты сглаживаются и поэтому расстояния, измеренные на карте, всегда получаются меньше действительных.
Измерение площадей. На какой площади раскинулся город, сколько гектаров занимают различные угодья, какова площадь озера - на все эти вопросы может ответить карта. Нужно только знать приемы измерения площадей. Один из них заключается в следующем. На контуре, в пределах которого требуется определить площадь, на глаз строят равновеликий прямоугольник. Измерив его основание и высоту и перемножив одно на другое, получим площадь фигуры. Для более точных определений фигуру разбивают на сеть прямоугольников, квадратов и треугольников. Площадь каждого из них вычисляют по известным правилам геометрии. Сумма площадей отдельных фигур даст общую площадь, заключенную в контуре.
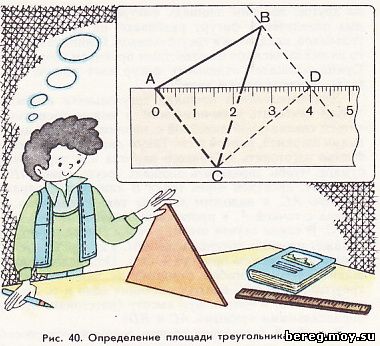
Для определения площади треугольника необязательно прибегать к вычислениям, а можно воспользоваться специальной линейкой с миллиметровыми делениями шириной, равной 2 см. Такую линейку вы можете быстро изготовить из тонкого картона или чертежной бумаги. Чтобы определить площадь треугольника АВС (рис. 40), проведем через точку В линию BD, параллельную АС, и наложим линейку так, чтобы нуль ее совпал с точкой А, а противоположный край - с точкой С. В таком случае отсчет у точки D в сантиметрах покажет площадь треугольника АВС в квадратных сантиметрах (в нашем примере 4 см²). Определение площади данным способом основано на равновеликости треугольников АВС и ADC, имеющих одно и то же основание (АС) и одинаковую высоту (расстояние между параллельными прямыми АС и BD).
В учебной литературе обычно рекомендуют способ определения площади по сетке квадратов, нанесенной на прозрачную бумагу или пленку. Стороны квадратов должны быть такими, чтобы каждый из них соответствовал целому числу гектаров или квадратных километров. Так, для карт масштабов 1:25 000, 1:250 000 и 1:2 500 000 квадраты вычерчивают со стороной 4 мм. Для первой карты в квадрате будет содержаться 1 га, для второй - 1 км² и для третьей - 100 км². Прикладывая такую сетку на контур карты, подсчитывают число квадратов, покрывающих площадь, причем доли квадратов определяют на глаз.
Подумайте, можно ли этот способ упростить. Допустим, заданная площадь точно ограничена одним квадратом. Но ведь этот квадрат можно обозначить точкой, стоящей в его центре! Значит, квадратную сетку можно заменить точечной. Количество точек в пределах контура будет соответствовать числу квадратов, и здесь уже не нужно подсчитывать число долей квадратов. Кроме того, точечную сетку легче изготовить. Возьмите кусок восковки, наложите его на лист из тетради в клетку и отметьте точками вершины клеток. Ваша палетка готова к работе. Только сообразите, какой площади будет соответствовать каждая точка, например, для карт масштабов 1:100 000, 1:1 000 000 и 1:10 000 000.
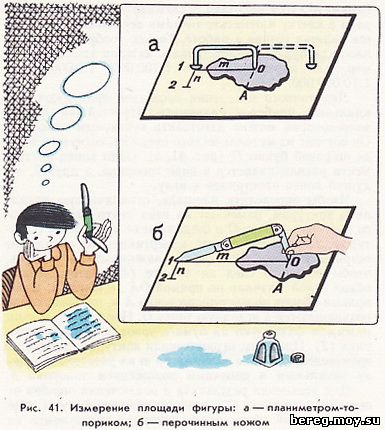
Для точного измерения площадей применяют специальный прибор - планиметр. Простейший планиметр-топорик можно изготовить кустарным способом. Он состоит из металлического стержня, согнутого в виде широкой буквы П (рис. 41, а). Один конец инструмента расплющивается в виде топорика, а другой, ведущий конец заострялся в иглу.
Чтобы определить площадь, ограниченную каким-либо контуром, намечают на глаз центр тяжести этого контура - точку О и соединяют ее прямой ОА с контуром. Планиметр ставят в вертикальное положение острием в точку О и слегка нажимают на топорик, чтобы получить след на бумаге (1). Затем делают обвод иглой, сначала по прямой ОА до контура, далее полный оборот по контуру до точки А и, наконец, снова возвращаются в исходную точку О. После этого легким нажимом фиксируют на бумаге новое положение топорика (2). Площадь, ограниченная контуром, равняется произведению длины планиметра и на расстояние между начальным и конечным положением топорика п.
Для уточнения результата и исключения ошибки от несовпадения точки О с центром тяжести фигуры надо сделать новый обвод после поворота инструмента на 180°, как показано пунктиром, и в противоположном направлении. За окончательный результат принимают среднее положение из двух полученных значений. С помощью такого простого прибора вы можете измерять площади с точностью до 2 - 3%.
Планиметр-топорик можно заменить перочинным ножом с двумя лезвиями (рис. 41, б). Точность определения площади с помощью ножа будет несколько ниже, но зато нож всегда может оказаться у вас под руками.
Определение географических координат. Многие задачи по карте решаются с помощью градусной сетки. Она служит не только канвой для нанесения на карту элементов ландшафта, но и позволяет определить географические координаты любого пункта или нанести на карту пункт по его координатам и тем самым узнать, где он расположен. Задачи эти чисто практические и очень интересные. Как же они решаются?
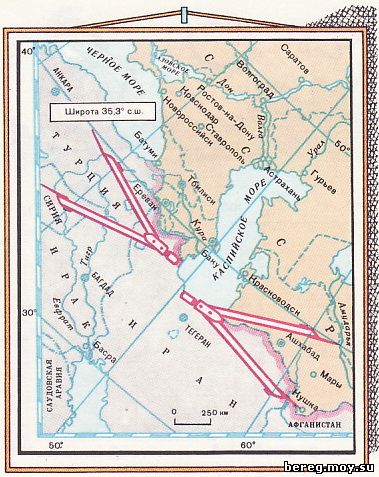
Рис. 42. Определение по карте географической широты
Большинство карт в школьных географических атласах составлены в конической проекции. Параллели изображены на них дугами концентрических окружностей, а меридианы - расходящимися прямыми линиями. У рамки карты даны подписи параллелей и меридианов и помешены градусные шкалы для отсчета координат. Но как неудивительно, ими многие не умеют пользоваться, особенно шкалой для определения широт. Обычно измеряют отрезок от пункта до параллели с меньшим отсчетом и пытаются его как-то отложить на широтной шкале, но из этого ничего не получается. На самом деле нужно брать отрезок от пункта до параллели с большим отсчетом, как это показано на рисунке 42. Затем этот отрезок прикладывают к западной или восточной стороне рамки так, чтобы одна игла помещалась на градусной шкале, а вторая - в точке касания с той же параллелью, до которой измеряли расстояние, и производят по шкале отсчет. В примере на рисунке широта самого южного пункта нашей страны - Кушки получилась равной 35,3°. При отсутствии циркуля-измерителя можно воспользоваться линейкой или полоской бумаги. Долготу пункта можно определить с помощью линейки, приложив ее так, чтобы прямая линия проходила через заданную точку и одинаковые отсчеты долгот по градусным шкалам на северной и южной сторонах рамки. Отсчет долготы в северном полушарии лучше делать по шкале на южной стороне, так как интервалы там больше и отсчеты получаются точнее.
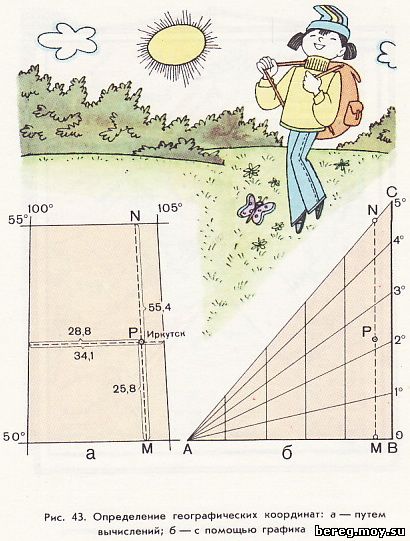
В общем случае и с большей точностью координаты определяют путем несложных расчетов. Допустим, нам надо определить координаты Иркутска (рис. 43, а). Найдем градусную клетку, где расположен город, и узнаем широту нижней и верхней параллелей, а также долготу левого и правого меридиана. Через центр условного знака города проведем линии, параллельные ближайшему меридиану и ближайшей параллели. По этим линиям измерим расстояния между меридианами и параллелями и расстояния от параллели и меридиана с наименьшими отсчетами до заданного пункта. Для определения его координат составим и решим пропорцию: 55,4 мм - 5°, 25,8 мм - х. х = 25,8х5/55,4 = 2,3°.
Широта Иркутска получилась равной 52,3° в. д. Таким же способом вычисляют и долготу.
Если вам придется измерять координаты нескольких пунктов, полезно изготовить график, который в значительной мере упростит работу. На листе клетчатой бумаги постройте прямоугольный треугольник АВС (рис. 43, б). Длина катета АВ произвольная, а катет ВС должен быть немного больше любого отрезка между меридианами и параллелями на карте. Поделите линию ВС на пять равных отрезков, обозначающих градусы, и точки деления соедините с точкой А. Параллельно катету ВС проведите ряд линий, и ваш график готов. Использование его для определения координат покажем на том же примере. Возьмем с карты отрезок между параллелями MN и уложим его на графике параллельно вертикальным линиям. На этом отрезке отложим расстояние от точки М до пункта и у полученной точки Р возьмем отсчет (целые градусы у нижней наклонной линии, а десятые градуса на глаз). Он получился у нас равным 2,3°, т. е. точно таким же, как и при вычислении.



