Кратчайший путь. Линия наиболее короткого расстояния между двумя пунктами земного шара совпадает с дугой большого круга и называется ортодромией, что значит «прямобегущая». Ортодромию можно построить на карте с помощью глобуса. На нем отмечают начальный и конечный пункты и к ним прикладывают нить, которая и пойдет по дуге большого круга. Чтобы перенести ортодромию на карту, определяют широту точек пересечения нити со всеми меридианами. Такие данные для трассы, например, Москва - Гавана помещены в таблице. 

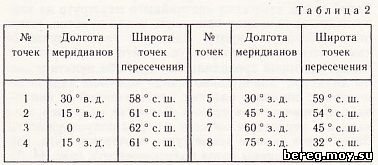
 По этим координатам нанесите на карту точки, а затем соедините их плавной кривой. Полученная линия, хотя на карте и является кривой, на самом деле укажет трассу кратчайшего воздушного пути самолетов, следующих из Москвы в Гавану и обратно.

 Итак, кратчайшая линия между двумя точками изображается кривой, прямая же не является кратчайшей. Это звучит как парадокс для нас, вынесших из учебника геометрии совершенно иные представления. Но школьная геометрия изучает свойства фигур, расположенных на плоскости. Мы же имеем дело с шаровой поверхностью. 

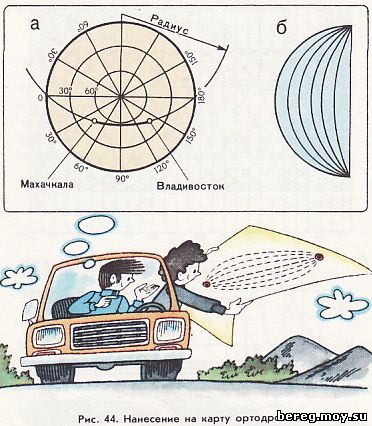
 Если у вас имеется карта северного полушария, составленная в азимутальной равнопромежуточной проекции, то при решении подобных задач можно обойтись без глобуса. Допустим, вы хотите узнать кратчайший путь между городами Махачкала и Владивосток, широта которых почти одинакова (рис. 44, а). Возьмите циркуль и, передвигая его иглу вдоль линии меридиана, расположенного посередине между пунктами, подберите такой радиус, чтобы дуга окружности проходила через оба пункта и опиралась на диаметр полушария. Кратчайший путь в нашем примере проходит по дуге, показанной на рисунке утолщенной линией. Такой прием нанесения кратчайшего маршрута на карту полушария можно применить и для пунктов, имеющих различную широту. Однако в таком случае не так-то легко подобрать радиус и найти центр окружности, дуга которой проходила бы через оба пункта и концы диаметра. Значительно проще подобные задачи решаются с помощью палетки, изготовленной из какого-либо прозрачного материала. Возьмите, например, лист кальки и перенесите на него с карты полуокружность. Затем через равные промежутки прочертите дуги, соединяющие вершины углов полуокружности (рис. 44, б). 

 Чтобы определить кратчайший путь между двумя какими-либо пунктами, совместите линию полуокружности на палетке с линией окружности на карте. Поворачивая палетку вокруг центра полушария, добейтесь такого положения, когда оба пункта окажутся на одной какой-либо дуге меридиана. По этой дуге и будет проходить кратчайший путь. Нужно только еще раз проверить, точно ли совмещена линия полуокружности на палетке с окружностью полушария. 

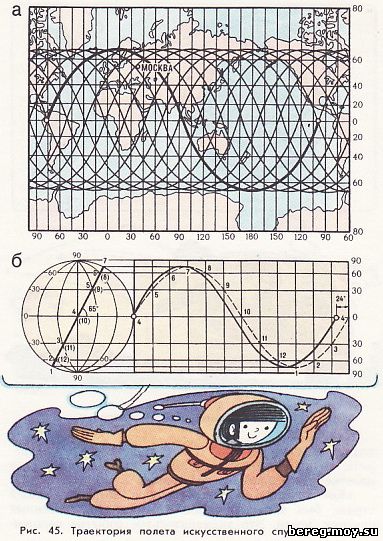
 Космическая» задача. В октябре 1957 года в нашей стране был запущен первый в мире искусственный спутник Земли. Это знаменательное событие положило начало космической эре в истории человечества. Рисунок 45, а воспроизводит орбиту первого советского спутника на карте мира в проекции Меркатора. Почему же она изобразилась не одной прямой, а целым рядом кривых линий и почему эти кривые имеют странную форму с поворотами, тогда как спутник двигался в одном направлении вокруг Земли? Для решения этой задачи воспользуемся другой картографической проекцией с густотой градусной сетки в 30° (рис. 45, б). Это сделано для наглядности построения чертежа и на решение нашей задачи не окажет никакого влияния. 

 Плоскость орбиты первого искусственного спутника Земли была наклонена к плоскости земного экватора под углом 65°. Построим ее след на проекции земного шара в виде прямой линии 1 - 7. На этой линии пометим точки пересечения параллелей с соответствующими меридианами и обозначим их на прямой стороне проекции шара от 1 до 7 и на обратной от 8 до 12. Спроецируем все намеченные точки на картографическую сетку и соединим их плавной пунктирной линией. Получилась траектория движения спутника при условии, что плоскость его орбиты не участвует в суточном вращении Земли. 

 Теперь внесем поправку за вращение Земли. Первый советский спутник совершал полный оборот вокруг планеты примерно за 96 мин. За это время Земля, вращаясь с запада на восток, повернулась на 24°. Эта величина определяется из пропорции 96/1440 = х/360°; х = 360х96/1440 = 24°, где числа левого отношения представляют собой период обращения спутника (96 мин) и суточного вращения Земли (1440 мин). Разница в 24° накапливается за время одного оборота спутника. Совершив полный оборот вокруг планеты, он попадает не в начальную точку витка, а на 24° западнее. Траектория спутника с учетом вращения Земли показана на рисунке 45 сплошной линией. 

 С каждым следующим оборотом спутника его траектории будет смещаться на 24° и через 15 оборотов (360:24) вновь пойдет по начальному следу. Проекции этих 15 витков и нанесены на общей схеме движения спутника на рисунке 45, а.