Материки, пойманные в координатные сети. Глобус, безусловно, дает самое верное представление о взаимном расположении материков и океанов, рек, городов, гор. Но с этой моделью нашей планеты не очень удобно работать. Глобусы при всех своих достоинствах очень мелкомасштабны и громоздки. Кроме того, на нем трудно производить линейные измерения, определять плановые координаты точек, наносить на него изображения географических объектов. Да и пользоваться глобусом не всегда удобно. Поэтому-то глобусы имеют меньшее распространение и применение, чем карты, которые более удобны для использования и хранения. 

 Как же перейти от глобуса к карте, как перенести сферическую поверхность Земли на плоскость?

 На помощь приходит градусная сетка. Ее можно как угодно трансформировать, а затем с глобуса по клеткам перенести контуры материков. Сущность такого преобразования легко уяснить из рисунка 24, где показан профиль лица, заключенного в различные сетки. Будем считать, что первый рисунок представляет собой реальный вид. Какие же изменения произошли с профилем на втором рисунке? Весь профиль сделался скошенным, подбородок выдался вперед, а затылок назад и т. д. Чем детальнее мы станем описывать результаты, тем яснее будем ощущать, как помогает такому описанию измененная сетка. В сущности, все описания можно свести к показу того, что произошло с сеткой: ведь все детали изображения, как в каркасе, остались в своих клетках. 

 Подобные преобразования происходят и на карте. Нужно только перенести каким-то способом градусную сетку с глобуса на лист ватмана, т. е. на плоскость. А после того как сетка станет плоской, на нее уже нетрудно нанести очертания материков, реки, города и другие точки по их географическим координатам. 

 Как перенести градусную сетку с глобуса на плоскость? Возьмем полый стеклянный шар и на одной его половине нанесем градусную сетку. Установим шар против экрана и с другой стороны на уровне экватора поместим источник света, например карманный фонарь. На экране получится градусная сетка, подобная той, которую мы привыкли видеть на карте полушарий. Обведем ее и сравним с градусной сеткой глобуса. 

 Если на глобусе все параллели представляют собой окружности, расположенные параллельно экватору, то на карте полушария экватор изображается прямой линией, а параллели - кривыми линиями разной округлости. Поэтому равные расстояния между параллелями получаются на карте различными. Все меридианы на глобусе имеют одинаковую длину, что соответствует действительности. На карте полушария длина меридианов различна. Средний меридиан изображен прямой линией, остальные - кривыми, и крайние меридианы образуют окружности, длина которых в полтора раза больше среднего. 

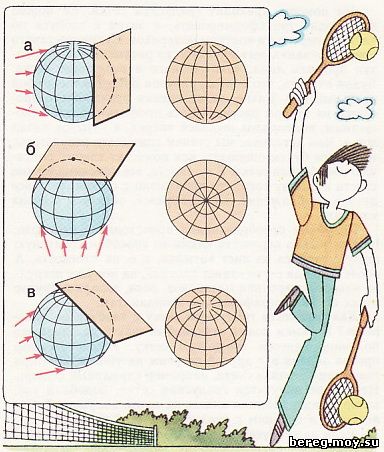
Рис. 25. Азимутальные проекции: а - поперечная (экваториальная); б - нормальная (полярная); в - косая

 Вот так мы преобразовали градусную сетку, и в результате у нас получилась одна из так называемых азимутальных проекций. Данная проекция является поперечной, потому что плоскость, на которую проектируется градусная сетка, расположена поперек плоскости экватора (рис. 25, а). Если же обе плоскости будут параллельными, то такую проекцию называют нормальной (рис. 25, б). Градусная сетка в нормальной азимутальной проекции принимает совсем иной вид. Параллели изображаются концентрическими окружностями, а меридианы - радикальными прямыми, исходящими из полюса. 

 Плоскость, на которую проектируется градусная сетка, можно расположить и по-другому. Она может, например, касаться глобуса в какой-нибудь точке, лежащей между полюсом и экватором (рис. 25, в). И опять новая - косая азимутальная проекция, совсем непохожая на две предыдущие. Здесь параллели и меридианы весьма наглядно подчеркивают сферичность земного шара. Карта в этой проекции встречается не только в географических атласах и школьных учебниках. Вспомним герб нашей Родины. Там тоже увидите карту, составленную в косой азимутальной проекции. Земной шар, изображенный на гербе, благодаря такой проекции выглядит очень эффектно. Он представляется как бы силуэтом нашей планеты, летящей в пространстве. 

 Сколько может быть проекций? Вы уже знаете, что азимутальные проекции получаются проектирующими лучами, исходящими из одной точки - центра проекции. Теперь представьте, что центр проекции будет в бесконечном удалении от глобуса и, следовательно, проектирующие лучи станут взаимно параллельными. Как же в этом случае будут выглядеть параллели в поперечной проекции? 

 Вспомним, что параллели на глобусе проходят параллельно экватору. Экватор в нашей проекции изображается прямой линией. Значит, все параллели будут изображены также прямыми линиями, параллельными экватору. Таким образом проекция видоизменилась. А сколько будет ее разновидностей по мере того, как центр проекции постепенно перемещается все дальше и дальше от глобуса? Бесконечное множество, где каждая новая проекция будет отличаться прежде всего кривизной параллелей. 

 Мы рассмотрели разновидности только одной проекций - поперечной азимутальной, а их существует очень много. Градусную сетку можно проектировать не сразу на плоскость, а вначале на поверхность конуса или цилиндра, которую затем разрезают по образующей линии и развертывают в плоскость. Такие проекции называют коническими и цилиндрическими. 

 Сущность проектирования градусной сетки с глобуса на поверхность конуса или цилиндра обычно поясняют с помощью таких же рисунков, которые мы приводили при знакомстве с азимутальными проекциями. Сейчас мы дадим другое представление о них, наглядно показывающее, как из азимутальной нормальной проекции получается коническая, а из конической - цилиндрическая. 

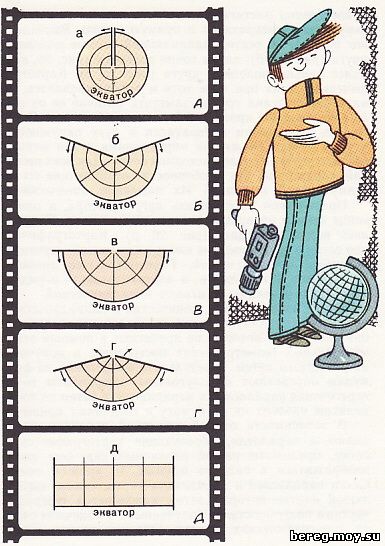
Рис. 26. Переход от азимутальной проекции (а) к коническим (б, в, г) и цилиндрической (д)

 Допустим, у нас имеется круг из какого-то деформирующегося материала, на котором показана картографическая сетка в азимутальной проекции (рис. 26, а). По одному из радиусов-меридианов круг разрываем и постепенно растягиваем его так, чтобы экватор из окружности превратился в прямую линию. Вначале у нас получается сектор, занимающий больше половины круга (рис. 26, б), затем точно полкруга (рис. 26, в) и далее меньше половины круга (рис. 26, г). Картографическая сетка при этом хотя и деформировалась, но на первый взгляд трудно заметить отличие ее от сетки азимутальной проекции. А такое отличие есть. Экватор из окружности превратился в дугу окружности, а углы между смежными меридианами стали меньше соответствующих углов исходной сетки. Для всех проекций характерны эти особенности, отличающие их от азимутальной проекции. Их называют коническими. 

 Продолжаем распрямлять дугу экватора, и она в конце концов превращается в прямую линию. Получилась новая проекция (рис. 26, д). Картографическая сетка в этой проекции имеет вид взаимно перпендикулярных прямых линий. Горизонтальные линии - это экватор и параллели, а вертикальные - меридианы. Такую проекцию называют цилиндрической. 

 Кроме азимутальных, конических и цилиндрических проекций, существуют очень много других проекций, при построении которых не прибегают к помощи вспомогательных геометрических построений, а получают их расчетным путем. В результате вычислений по формулам определяют прямоугольные координаты точек пересечения параллелей и меридианов, а затем по координатам наносят их на бумагу и соединяют кривыми. 

 В зависимости от той или иной проекции меридианы и параллели, образующие картографическую сетку, принимают самый различный вид: они могут изображаться в виде то прямых, то кривых линий. Сетка параллелей и меридианов - это основа, каркас любой карты, которая затем наполняется географическими подробностями, полученными в конечном счете из топографических съемок. Образно говоря, сетка служит канвой, на которой вышиваются географические узоры. 

 Разные проекции - различные искажения. У одного древнегреческого историка имеется рассказ о разбойнике Прокрусте. Горе было путнику, который попадал в его руки. Прокруст укладывал его на свое ложе, и, если жертва оказывалась короче кровати, он вытягивал ей ноги, если длиннее - отрубал. Слова «прокрустово ложе» стали крылатым выражением. Мы вспоминаем о них тогда, когда говорим о каких-либо рамках, в которые нельзя уложить явления живой и многообразной действительности. Между тем эти рамки мы не всегда вольны расширить и нередко, принося в жертву второстепенные признаки того или иного явления, сберегаем наиболее важное и ценное для нас. 

 Плоское изображение в известной мере является тоже «прокрустовым ложем» для географических объектов, расположенных на сферической поверхности. Искажения, возникающие на карте, являются расплатой за удобство, которое мы получаем при пользовании плоским изображением. Характер искажений на картах зависит от вида картографической сетки, так как в нее, как в «прокрустово ложе», приходится вгонять изображения материков. Вот почему на разных картах получаются различные искажения. На одних картах сильно искажается соотношение площадей, но сохраняется равенство углов. Такие проекции называют равноугольными. Другие карты, наоборот, отличаются тем, что сохраняют соотношение площадей, но сильно искажают конфигурацию материков. Они называются равновеликими. Сохранение площадей в равновеликих проекциях получается за счет искажения углов, а следовательно, в очертаниях самих изображений, и, наоборот, сохранение углов в равноугольных проекциях приобретается ценой искажения площадей. Вообще говоря, чем больше искажения углов, тем меньше искажения площадей, и наоборот. Проекции, которая была бы одновременно равноугольной и равновеликой, нет и быть не может. Здесь уместно привести четверостишия, составленные известным картографом А. В. Гедыминым: 

Изучая суть проекций, 
Надо помнить положение: 
С переходом сферы в плоскость 
Неизбежны искажения. 

Карты вовсе не безгрешны 
И в пределах разных норм 
Нарушают верность линий, 
Площадей, углов и форм. 

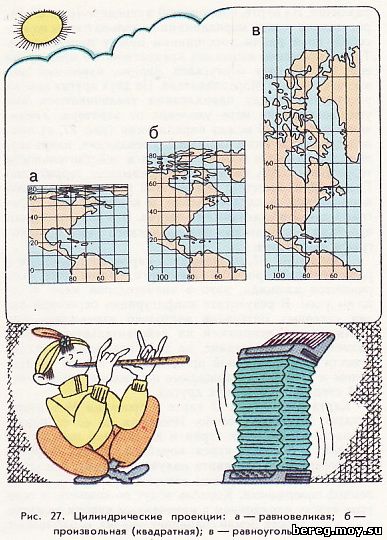
 На рисунке 27 показаны вырезки из трех карт мира. Все они составлены в цилиндрической проекции, но их картографические сетки имеют существенные различия. На карте, помещенной в середине (рис. 27, б), расстояния между меридианами не только равны между собой, но и равны расстояниям между параллелями. Такую проекцию называют квадратной. Ее предложил еще в 1438 году португалец Энрико, известный под именем Генриха Мореплавателя. На двух других картах расстояния между параллелями увеличиваются или уменьшаются по мере удаления от экватора. Увеличение расстояний между параллелями (рис. 27, в) приводит к искажениям площадей. Гренландия, например, выходит на карте больше США, а в действительности территория США значительно превышает территорию Гренландии. Вместе с тем на этой карте сохраняются направления, а следовательно, и конфигурация береговых линий в отдельных ее частях. Это равноугольная проекция, носящая имя нидерландского ученого-картографа Меркатора. 

 Слева (рис. 27, а) помещена карта, составленная в равновеликой проекции Ламберта. Здесь уже сохраняются площади, зато в значительной мере искажены углы. В результате конфигурация береговой линии северных материков настолько изменилась, что стала совсем непохожей на действительную. Карту, размещенную в середине, по виду искажений следует отнести к произвольной проекции, так как ей свойственны и угловые и площадные искажения, но в меньшей степени, чем в двух других. 

 Карта Меркатора. О карте в проекции Меркатора следует поговорить особо. Несмотря на ее солидный возраст, моряки всех стран и до сих пор пользуются ею для прокладки курса кораблей. Такое широкое распространение эта карта получила потому, что углы, измеренные на ней, равны соответствующим углам на земной поверхности. Корабль ведут по компасу, и если угол между меридианом и намеченным курсом на карте и на поверхности Земли совпадает, значит, корабль идет точно по курсу. Какую же особенность имеет карта Меркатора? 

 Обратимся опять к рисунку 27. В квадратной проекции искажения береговых линий материков особенно заметны потому, что при сохранении единого масштаба вдоль меридианов масштаб параллелей нарастает, достигая огромных размеров вблизи полюсов. Меркатор решил пропорционально растяжению параллелей между меридианами увеличивать и отрезки самих меридианов. В этом случае, хотя и пришлось поступиться сохранением единого масштаба вдоль меридианов, все же удалось сохранить подобие фигур небольших участков земной поверхности, их действительные, неискаженные очертания. А в подобных фигурах углы остаются соответственно одинаковыми. Понятно, что при переходе к большим фигурам подобие и здесь нарушалось. 

 Итак, Меркатор дополнительно растянул отрезки меридианов в определенной последовательности: чем ближе к полюсу, тем большее растяжение испытывает очередной отрезок меридиана. Однако, если бы он довел свою работу до полюсов, создалось бы крайне сложное положение. У полюсов, меридианы стали бы бесконечно длинными, и поэтому Меркатор срезал карту сверху и снизу, отбросив приполярные области. Кстати сказать, очертания их тогда были известны крайне неточно и неполно, и спроса на карты этих территорий, естественно, не было. И все же в юго-западном углу карты Меркатор поместил врезку, на которой изображен район, прилегающий к Северному полюсу. Разумеется, карта-врезка составлена в другой, азимутальной проекции. На ней показаны четыре больших острова с проливами между ними. В легенде приводятся источники, послужившие для такого изображения. Меркатор ссылается на отчет путешествия некого Якова Кноена. Возможно, такое путешествие было, но не к истинному географическому, а к магнитному полюсу. Заблуждение легко объяснимо: в то время еще не знали о магнитном склонении и полагали, что стрелка компаса направлена на истинный север, а магнитный полюс как раз и находится в островной группе Канадской Арктики. 

 Перекрытие изображений на карте мира. Большинство карт мира составляют в произвольных проекциях. Они не дают на карте резких искажений в очертаниях материков и их площадей. Но для политической карты мира обычно применяют равновеликую проекцию, так как на карте очень важно показать правильное соотношение площадей различных стран. Эта карта, как правило, заключена в прямоугольную рамку, и в ее углах повторяется изображение одной и той же территории, где особенно резко выделяются угловые искажения, т. е. искажения в очертании материков. 

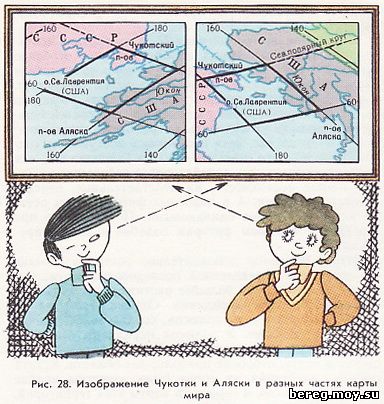
 На рисунке 28 показаны вырезки из северо-западного и северо-восточного углов политической карты мира. На правой и левой вырезках выделена клетка градусной сетки, ограниченная двумя одноименными меридианами (180° и 160° з. д.) и параллелями (60° с. ш. и Северным полярным кругом). Соответствующие стороны обеих клеток имеют почти одинаковые размеры, и поэтому площади одноименных островов и полуостровов на той и другой вырезке будут практически равны. Вместе с тем искажения в направлениях очень велики. Если на левой вырезке угол между параллелью и меридианом острый, то на правой вырезке он будет тупым, и наоборот. Соответственно искажены и углы с любого пункта на однозначные объекты. Все это сказывается на конфигурации полуостровов, островов, рек. Сравните, например, изображения полуострова Аляски на правой и левой вырезках. Они настолько непохожи друг, на друга, что на первый взгляд их трудно сопоставить. Обратите внимание на остров Св. Лаврентия. На левой вырезке он сплюснут, а на правой вытянут, и нет никакого подобия между этими двумя изображениями одного и того же острова. 

 Карты с разрывами. Подумайте, как можно уменьшить искажения на картах. Путь к решению этого вопроса есть: надо проектировать поверхность земного шара не всю сразу, а по частям. В таком случае между отдельными частями получатся разрывы, но зато в каждой части искажения будут небольшими. В этом вы можете убедиться, проделав следующий опыт. Снимите кожуру с апельсина целиком и распластайте ее на столе. Что же у вас получилось? Сферическая поверхность апельсина развернулась в плоскость, но произошло это за счет образовавшихся разрывов. Этот простой, но интересный опыт вы можете проделать несколько раз и даже усложнить его, нарисовав на поверхности апельсина «параллели и меридианы». Разные варианты снятия кожуры приведут к различным формам отдельных частей поверхности, а линии сетки в местах разрывов будут также разорваны, а далее пойдут в другом направлении. 

 Для карт мира можно сделать разрывы в океанах, и тогда формы и размеры материков будут изображены более точно. 

 Применяют и другие варианты. На рисунке 29 показана необычная проекция Мирового океана. Разрывы здесь идут по материкам, и это дает возможность изобразить поверхность морей и океанов без значительных искажений площадей. Но чтобы этого добиться, пришлось пожертвовать точностью изображения материков. Их очертания сильно искажены, разорваны. 

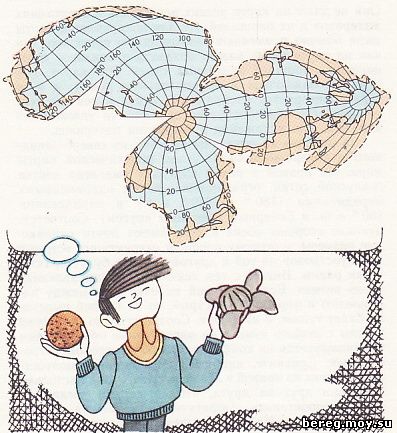
Рис. 29. Карта Мирового океана с разрывами по материкам

 Карта полушарий - это та же карта мира, но разорванная на две равные части. В результате такой проекции максимальное искажение в каждом полушарии будет значительно меньше, чем на целой карте мира. 

 Карту с разрывами можно получить из «выкроек» глобуса. Она будет состоять из 12 меридиональных долек, сложенных так, чтобы все они соприкасались между собой по линии экватора. Искажения в каждой дольке будут очень малыми: ведь если все их склеить, то получится глобус, т. е. фигура, подобная земному шару.

 Таким же путем и получается проекция топографических карт. Дольки здесь очень узкие - всего по 6° долготы, и в каждой из них по параллелям через 4° широты нарезают листы карты масштаба 1:1 000 000. В результате такого проектирования масштаб карты в пределах каждого листа будет практически одинаков, как на плане. 

 Вы можете спросить: значит, все же есть карта без искажений? Нет, топографическая карта также имеет искажения, но они скрыты между ее отдельными листами. 

 Выявить это очень просто. Возьмем четыре смежных листа миллионной карты, обрежем поля и попытаемся сложить их в один большой лист карты. Три любых смежных листа прикладывают друг к другу точно, а четвертый лист даст угловой разрыв между параллелями или меридианами. Разрыв небольшой: на широте Москвы он достигает у конца стороны всего 2 мм, а если его распределить по всем четырем сторонам, то становится совсем незаметным.